| Metal Sheath | Quartz Tube | Quartz Lamp | Catalytic | Flat Faced Panels | Ceramic | |
|
Radiant Efficiency
|
56%
|
61%
|
86%
|
80%
|
88%
|
96%
|
|
Physical Strength
|
High
|
Low
|
Very Low
|
High
|
Medium |
Medium
|
|
Heat-Up Cool-Down
|
Slow
|
Fast
|
Very Fast
|
Very Slow
|
Slow |
Slow
|
|
Max. Temp.
|
1400 °F
|
1600 °F
|
4000 °F
|
800 °F
|
1600 °F |
1292 °F
|
| Color Sensitivity | Low | Low | High | Low | Low | Low |
Physical Strength: The physical strength of each source. A high rating indicates a very durable source that can withstand physical abuse such as dropping a wrench on the source.
Heat-Up/Cool Down: The amount of time required for the source to come up to operating temperature and cool back down to room temperature.
Maximum Temperature: Maximum operating temperature of the source.
Color Sensitivity: Refers to the ability of a typical load to absorb the spectral radiation emitted from a source based on the color of the load. The shorter the wavelength emitted from a source the more color sensitive a load will be to the sources spectral radiation.
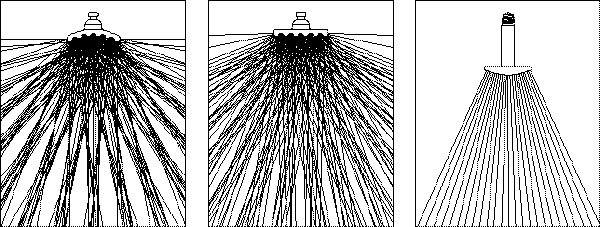
Concentrated Uniform Wide Area
Concentrated: The concave surface will emit a “concentrated” radiant pattern which is highly effective when zone heating is desired as well as radiant heating in general.
Uniform: The flat surface will produce a “uniform” pattern for even heating at a close proximity between the emitter and the target being heated.
Wide Area: The convex shape gives off a “wide area” pattern which is desirable in comfort heating or other applications that require a dispersed radiant emission pattern.
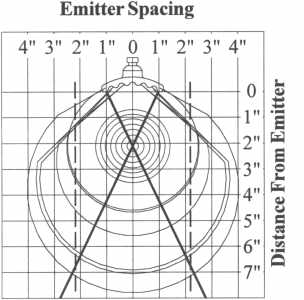
| Salamander Radiant Emission Grid
The Salamander radiant emission grid can be used to determine the proper ceramic emitter spacing when used in an application such as an infrared panel. In order to achieve an even heat pattern it is critical that the emitters are spaced so that their radiant emission patterns overlap when reaching the target. The more overlap that occurs, the more even the heat will be across the face of the product being heated. The area of highest radiant emission intensity for a single emitter is shown within the two dark crossed lines on the grid. In order for element emissions to overlap, the dashed line shows an intersection point at a distance of 7″ will occur if the emitters are placed a distance of 2″ apart from edge to edge. This same concept should be used to either determine the distance to place the product if using an existing panel, or placement of emitters if building a panel to guarantee radiant emission overlap.
|
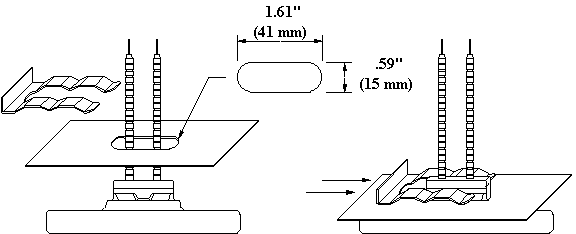
This drawing shows a ceramic heater and a reflector with an oblong hole for mounting.
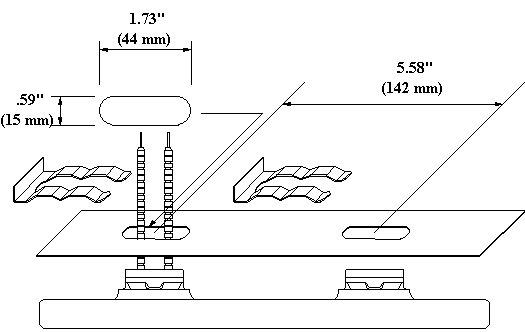
Our larger LTE element has two mounting posts on the back side. This drawing shows an LTE and a reflector with two oblong holes for mounting.

This drawing shows an LTE installed in a reflector.
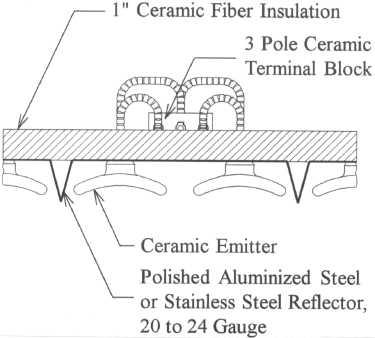
| High temperature 842°F (450°C) MG or similar style wire (with a suitable temperature and amperage rating) should be used for all electrical connections made within the terminal area of the infrared panel. The high temperature wire must be run on top of (or above) the ceramic fiber insulation. | |
| Ceramic terminal blocks are recommended to allow for quick emitter replacement, flexibility in zoning, and “touch safe” design. | |
| The terminal cover for the infrared panel should be louvered or made out of expanded metal to minimize the temperature within the terminal area. |
| Emitters that are tightly spaced in an array will allow the target to be positioned close to the emitters and still result in even heating. The intensity and efficiency of the infrared radiation will be maximized and heat losses will be minimized. | |
| Emitters that are loosely spaced in an array will force the target to be positioned further away in order to achieve even heating. This style of panel would typically result in a lower intensity infrared emission. |
Infrared Energy:
ρ = reflectivity
α = absorptivity
t = transmissivity
Example: Infrared energy strikes an object that is 30% reflective, and 20% transparent, how much infrared energy is absorbed by the object?
α = 1 – .30 -.20 = .50 (or 50% )
Emissivity:
Ws
e = _____________
Wbb
e = emissivity of source
Ws = Total radiant energy emitted from a source at temperature T1
Wbb = Total radiant energy emitted from a blackbody at temperature T1
c
λ = _______
f
λ = Wavelength in meters
c = Speed of light ( 3 x 108 meters per second )
f = Frequency in hertz ( cycles per second )
σ = Stefan-Boltzmann Constant
[ 36.58072 x 10 -12 W/ in2 K]
e = Emissivity Value of the Source
T = Surface Temperature of the Source in K (Kelvin.)
In order to understand the spectral distribution of infrared radiation from a source we must first understand Planck’s Law. Planck’s Law gives us the spectral distribution of radiation from a blackbody source. That is, a source that emits 100% infrared radiation at a given single temperature. It is important to understand at this point that in practice, infrared sources are made up of thousands of “point sources” that are all at different temperatures. Each point source will have a different spectral distribution and the combination of point sources will make up the entire spectral distribution. Therefore, we can only approximate the spectral distribution using an average surface temperature and emissivity value.
(e) x ( 2.416069 x 10-25 ) Watts
R(λ) = _______________________________________________
( λ ) 5 [ exp .014408/λT – 1 ] in 2 . µm
Where:
e = Emissivity of Source
λ = Wavelength in Meters
T = Temperature in K (Kelvin)
K = (°F + 460) / 1.8
At Various Temperatures
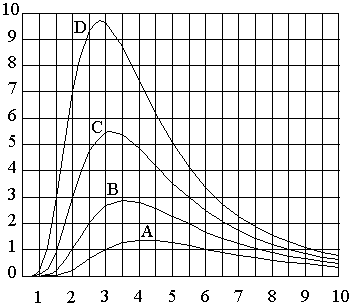
Wavelength, Microns (λm)
“A”….800 °F, λm = 4.14 mm “B”….1000 °F, λm = 3.57 mm
“C”….1200 °F, λm = 3.14 mm “D”….1400 °F, λm = 2.81 mm
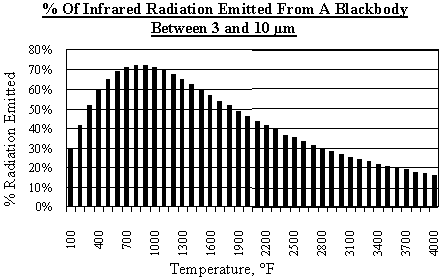
Also notice that as the temperature of the source increases, the peak wavelength of the source becomes shorter. When the temperature of the source becomes too high a noticeable amount of energy is emitted from the source as light. That is, a portion of the energy emitted from the source falls within the wavelengths associated with light. Referring back to the infrared spectrum chart shown on page 7, visible light occurs starting at .40µm and ends at .70µm. The infrared spectrum starts at .70µm and extends to 1000µm. Although the useful range of wavelengths for infrared heating applications occurs between .70µm to 10µm.
2.898 x 10 -3 m K
λm = __________________________
T k
λm = Peak Wavelength in Meters
T k = Temperature in K (Kelvin)
K = (°F + 460)/1.8
Surface Temperature and Radiation Emissions:
R = ( .80 )( 36.58072 x 10 -12 )[ (811)4] = 12.65 Watts / in2
at Various Emissivity Values
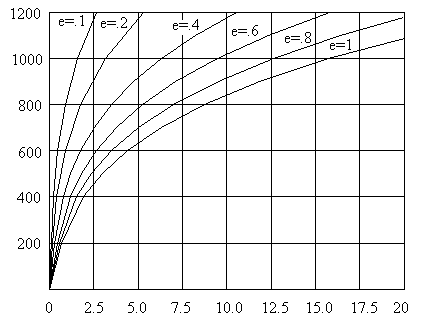 Watts / in2
Watts / in2
Single Emitter in 70 °F (21 °C) Ambient
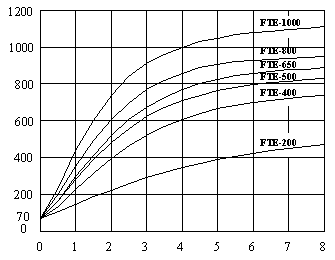 Time in Minutes
Time in Minutes
Surface Temperature Cool-Down Time:
Single Emitter in 70 °F (21 °C) Ambient
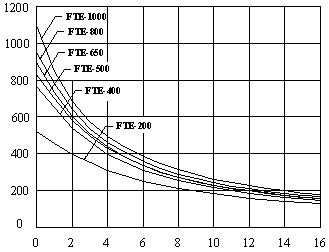 Time in Minutes
Time in Minutes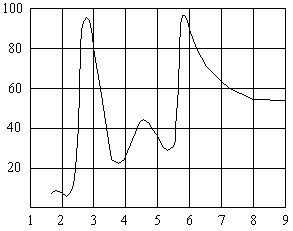
Wavelength, µm
Spectral Absorption Curve For PVC
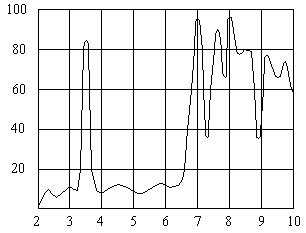
Wavelength, µm
Spectral Absorption Curve For Polystyrene
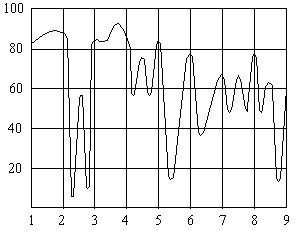
Wavelength, µm
Spectral Absorption Curve For Polyethylene![]()
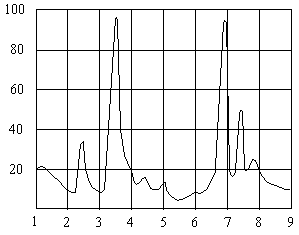
Wavelength, µm
| Material | Densitylb. / ft3 | Specific HeatBtu _______ lb.·°F |
Emissivity | Thermal ConductivityBtu · in _________ hr·ft2·°F |
Latent Heat of FusionBtu/lb. |
Latent Heat of EvaporationBtu/lb. |
Melting Point°F/°C |
Boiling Point°F/°C |
| Non-Metallic Solids: | ||||||||
| Asphalt | 65 | 0.40 | 0.93 | 1.20 | 40 | 250/121 | ||
| Beeswax | 60 | 1.67 | 75 | 144/62 | ||||
| Carbon | 138 | 0.20 | 165 | |||||
| Cotton | 92 | 0.31 | 0.77 | 0.41 | ||||
| Glass | 165 | 0.20 | 5.4 | |||||
| Ice | 57 | 0.53 | 32/0 | |||||
| Paper | 58 | 0.45 | 0.93 | 0.82 | ||||
| Paraffin | 56 | 0.70 | 1.56 | 63 | 133/56 | |||
| Rubber | 76 | 0.44 | 0.90 | 1.10 | ||||
| Wood, Oak | 50 | 0.57 | 0.90 | 1.15 | ||||
| Wood, Pine | 34 | 0.67 | 0.90 | 0.90 | ||||
| Plastics: | Most Non-Metals Have An Emissivity of 0.90 | |||||||
| ABS | 69-76 | 0.3-0.4 | ||||||
| Acrylic | 69-74 | 0.34 | ||||||
| Epoxy | 66-88 | 0.25-0.3 | ||||||
| Flouroplastic | 131-150 | 0.28 | ||||||
| Nylon | 67-72 | 0.3-0.5 | ||||||
| Phenolic | 85-124 | 0.35 | ||||||
| Polycarbonate | 74-78 | 0.30 | ||||||
| Polyester | 66-92 | 0.2-0.35 | ||||||
| Polyethylene | 57-60 | 0.54 | ||||||
| Polyamides | 90 | 0.27-0.3 | ||||||
| Polypropylene | 55-57 | 0.46 | ||||||
| Polystyrene | 66 | 0.32 | ||||||
| PVC | 72-99 | 0.2-0.3 | ||||||
| Metals: | ||||||||
| Aluminum | 169 | 0.24 | 1536 | 1190/643 | ||||
| – Polished | 0.09 | |||||||
| – Med. Oxide | 0.19 | |||||||
| – Heavy Oxide | 0.31 | |||||||
| 430 Stainless | 475 | 0.11 | 150 | 2650/1454 | ||||
| – Polished | 0.17 | |||||||
| – Med. Oxide | 0.57 | |||||||
| – Heavy Oxide | 0.85 | |||||||
| Liquids: | ||||||||
| Oil, Cottonseed | 60 | 0.47 | 0.90 | |||||
| Oil, Vegetable | 57.5 | 0.43 | 0.90 | 318/159 | ||||
| Paraffin | 47.1 | 0.71 | 750/399 | |||||
| Water | 62.4 | 1.0 | 0.93 | 4.08 | 965 | 212/100 |
Temperature:
°C = 5/9(°F -32) Or °F = 9/5(°C) +32
K = (°F +460)/1.8 Or K = °C + 273
°R = °F +460
Electrical:
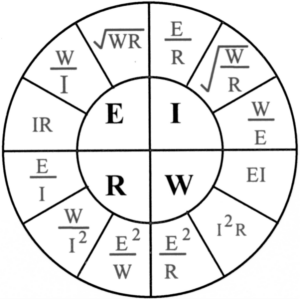
E = Volts, I = Amps
R = Ohms, W = Watts
| 3 Phase Wye (Balanced Load) | 3 Phase Delta (Balanced Load) |
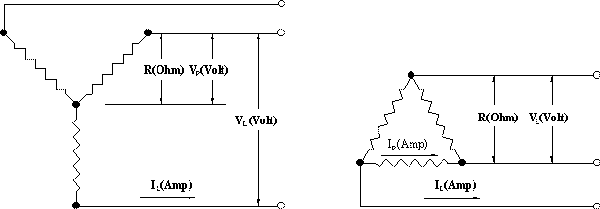 |
|
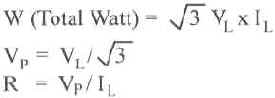 |
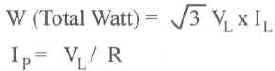 |
| 1 kW = 1000 Watt | 1 mm = .03937 Inch | 1 kg = 2.205 lb. |
| 3412 BTU = 1 kW-HR | 1 m = 39.37 Inch | 1 g = .002205 lb. |
| 1 HP = .746 kW | 1 Inch = 2.54 cm | 1 U.S. Gal. = 0.1337 Cu. Ft. |
| 1 Boiler H.P. = 9.8 kW | 1 km = .6214 Mile | 1 U.S. Gal. = 3.785 liters |
Thermoforming:
Calculations:
| Emissivity of the infrared source | = .90 |
| Emissivity of PVC Sheet | = .90 |
| Specific Heat of PVC | = .30 BTU / lb. / °F |
| Density of PVC | = 99 lbs. / ft3 |
| Temperature Required | = 350 °F (177 °C) |
| Ambient Temperature | = 65 °F (18 °C) |
lbs./in2 = (99 lbs./ft3)( 1/1728 in3)(.125 in) = .007161 lbs./in2
The power required to heat the PVC sheet is given by:
Watt-Hour (Weight)(Specific Heat)( T1 – T2 )
____________ = ____________________________________________
in2 3.412
(.007161)(.30)(350-65)
= _____________________________ = .179
3.412
Watt-Hour / in2
Warm-up Time = __________________ x 60 Minutes
Watt / in2
.179
1 min. = ________________ x 60
Watt / in2
Solve the “time” equation for Watt / in2:
(.179)(60)
Watt / in2 = ____________ = 10.74
1 min
Watt / in2 = 10.74
At this point one can use Planck’s Law and the spectral absorption curve for PVC by superimposing these curves on each other and calculating the total area under the curves at which the two curves intersect (provided that accurate curves are available). This can be extremely time consuming.
A simplified method of estimating the power radiated and absorbed into the PVC sheet is given by the following:
The effective emissivity between two parallel plates is given by:
1 1
e = __________________ = __________________
( 1/e1 + 1/e2 – 1) ( 1/.9 + 1/.9 – 1)
= .82
Two infrared heater panels will be used. One panel will heat the top of the PVC sheet, the other will heat the bottom of the PVC sheet. Heating both the top and bottom of the PVC sheet will minimize the temperature gradient within the sheet which could cause “part” deformation. Since two infrared panels will be used, the power required per panel is 1/2 of the 10.74 Watts / in2. Therefore, 5.37 Watts / in2 is required from each infrared panel.
Where:
T1= Source Temperature
T2 = Average PVC Temperature = (65+350)/2 = 208 °F
T2 = 371 K

= 667 K ( 741 °F or 394 °C)
Results:
The surface temperature of the source must be at least 741°F (394 °C) to achieve a 350 °F (177 °C) PVC sheet temperature within 1 minute.Water Evaporation:
Given: Estimate the amount of infrared radiation required to evaporate 4 grams of water per square foot every 5 seconds from a substrate material in a water based adhesive application. Assume the substrate to have a negligible mass.
Calculations:
| Emissivity of the infrared source | = .90 |
| Emissivity of Water | = .93 |
| Specific Heat of Water | = 1.0 BTU / lb. / °F |
| Latent Heat of Vaporization | = 965 Btu / lb. |
| Boiling Point of Water | = 212 °F (100 °C) |
| Ambient Temperature | = 65 °F (18 °C) |
Convert the grams of water per square foot to lbs. of water per square inch:(4 g/ft2)(.0022046 lb./g)( 1/144 ft2/in2) = 61.24 x 10-6 lbs./in2
The power required to heat the water is given by:
Watt-Hour (Weight)(Specific Heat)( T1 – T2 )
_______________ = __________________________________________
in2 3.412
(61.24 x 10-6)(1.0)(212 – 65)
= ______________________________________ = 2.64 x 10-3
3.412
(965 Btu/lb.)(61.24 x 10-6 lbs./in2)
Latent Heat of Vaporization = ______________________________________
3.412
= 17.32 x 10-3
Total Power Required = (2.64 x 10-3) + (17.32 x 10-3)
Watt-Hour
= 22.60 x 10-3 _____________
in2
Water Evaporation Example (continued):
Warm-up Time:
Watt-Hour / in2
Warm-up Time = __________________ x 60 Minutes
Watt / in2
(22.6 x 10-3)
5/60 min. = ________________ x 60
Watt / in2
Solve the “time” equation for Watt / in2:
(22.6 x 10-3)(60)
Watt / in2 = __________________ = 16.27
(5/60 min)
The effective emissivity between two parallel plates is given by:
1 1
e = __________________ = ___________________
( 1/e1 + 1/e2 – 1) ( 1/.9 + 1/.93 – 1)
= .84
Stefan-Boltzmann Law:
R = (.84)(36.58072 x 10 -12 )( ( T1 )4 – ( T2 )4 ) = 16.27
Where: T1 = Source Temperature
T2 = Average Water Temperature = (65+212)/2 = 138.5 °F (59 °C)
= 332.5 K
Solve the equation for the source temperature.
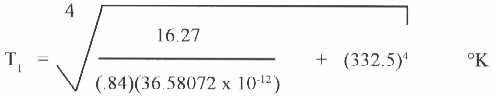
= 858 K = 1084 °F (584 °C)
Results: The surface temperature of the source must be at least 1084 °F (584 °C) to evaporate 4 grams of water within 5 seconds.


